What is spectroscopy?

Spectroscopy (NMR, IR, UV, Atomic adsorption) relies on the experimental observation that an atom or molecule can absorb electromagnetic radiation (energy).  When a molecule absorbs electromagnetic radiation (EMR) it invariably must change from some state of lower energy to a state of higher energy.  The various spectroscopic methods(IR, NMR, UV, etc.) differ by the way in which molecules can absorb EMR and the resulting state change.

There are different types of EMR and we characterize them by wavelength.  They make up the electromagnetic spectrum.  For example, x-ray's, infrared (IR), ultraviolet (UV), radiowaves (r_f) are all EMR having different wavelengths and photon energies.  Recall that the energy (E) of a photon is directly proportional to its frequency (ν) as follows;

E=hν

Here h is Plank's constant.

Recall also that frequency is related to wavelength (λ) as follows;

c=λν  

where c is the speed of light.  Therefore the energy of a photon is proportional to the inverse of its wavelength.

E=hc/λ

When will a molecule absorb electromagnetic radiation?

The requirement for a molecule to absorb EM is - the magnitude of the photons of EMR must exactly match some energy difference between two state of the molecule.

The difference in energy between the states of the molecule must exactly match the energy of the incoming electromagnetic radiation (or photon).

By now you all should have been exposed to the fact that energy on a very small scale is quantized.  This shouldn't be surprising since mass is obviously quantized (protons, neutrons etc.), so why should energy be any different....energy and mass are intertwined (E=mc²)!  Yeah its beyond the average chemist, but hey you just gotta take it as is.  In our everyday lives, we are used to non-quantized energies.  For example, I can drive my car at any speed I like.  Theoretically I could drive my car at 55 mph, or 55.126 mph or 57.8753 mph or whatever...there's an infinite number of speeds or energies(recall from physics E=1/2*mv²).  Well energy on a very small scale does not behave this way it is quantized into little bits.

Infrared (vibrational) Spectroscopy

For example, when a molecule vibrates it can only vibrate at certain distinct vibrational energies.  Although we will use the analogy of a spring to describe this on occasion, it is really a quantum mechanical spring.  It can only vibrate at certain frequencies.  Suppose the C=O bond below can vibrate at 1 Hz (hertz).  It's next allowed vibrational level maybe something like 4 Hz.  There is no in-between frequency of 1.5 or 3 allowed.  I made these numbers up for clarity but molecules actually vibrate at about 10¹² to approximately 10¹⁴ Hz.  Photons of EMR with this frequency lies in the infrared (IR) region, thus the reason for using IR radiation. 

+

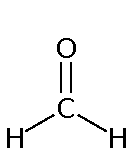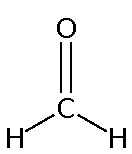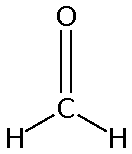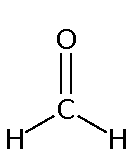hν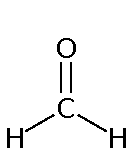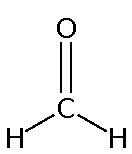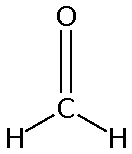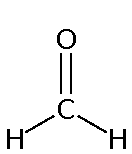

=

UV-Vis Spectroscopy

In UV spectroscopy the state changes are electronic.  Typically an electron is bumped (excited) from a low-lying HOMO to a higher energy LUMO MO when irradiated with UV EMR.  Since the HOMO LUMO differences is small in conjugated systems, they tend to absorb UV and visible radiation.  For example, Lycopene, the red component of tomatoes, is highly conjugated having 11 double bonds in conjugation.  Lycopene absorbs visible light strongly in the blue region and as a result, appears red in ripe tomatoes.

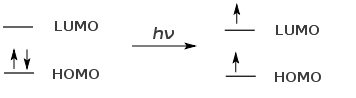
NMR Spectroscopy

In NMR spectroscopy its the different spin states result from placing nuclei in strong magnetic fields.  We will see that radio waves are utilized to energize the different quantized spins states.

Beer's Law

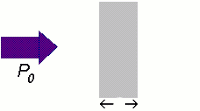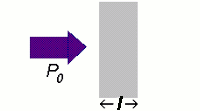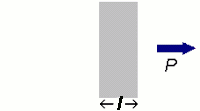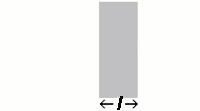
Beers law tells us that that the absorption (A) of light or EMR by a solution or material is directly proportional to the emissivity (ε), the distance the light travels through the material (l), and the concentration (c).  Whether most chemists realize it or not it's Beer's law that allows us to develop a standardization or calibration curve of absorbance (HPLC/UV, FTIR, Raman, etc) versus the concentration of an analyte.

The thicker the glass, the darker the brew, the less the light passes through.

A = εlc