Quick Menu

Huckel's 4n+2 Rule

The Hückel 4n+2 rule, also known as Hückel's rule or the Hückel aromaticity rule, is a simple rule to determine if a planar ring molecule will exhibit aromaticity. This rule is an essential concept in organic chemistry, particularly when dealing with the stability and reactivity of organic compounds. Aromatic compounds are notably stable and have unique chemical properties compared to non-aromatic compounds.

The rule is named after Erich Hückel, who proposed it in the 1930s. It states that a cyclic, planar molecule will be aromatic if it contains a total of 4n+2 π-electrons, where n is a non-negative integer (0, 1, 2, 3, ...). This rule is derived from quantum mechanical treatments but can be applied in a straightforward manner for predicting and explaining the stability of aromatic compounds.

Here's a breakdown of the criteria for a molecule to be considered aromatic according to Hückel's rule:

  1. Cyclic: The molecule must form a ring.
  2. Planar: The molecule must be able to lie flat, allowing all its atoms to be in the same plane.
  3. Conjugated: The molecule must have alternating single and double bonds, which allows for delocalization of π-electrons across the ring.
  4. 4n+2 π-electrons: The total count of π-electrons in the molecule must follow the 4n+2 formula. These π-electrons come from double bonds, lone pairs, or empty orbitals that are part of the conjugated system.

A classic example of a molecule that follows Hückel's rule is benzene, which has six π-electrons n=1 in the 4n+2 equation, giving 4(1)+2=6. Benzene is highly stable, which is a hallmark of aromaticity.

In contrast, molecules that have 4n π-electrons (where n is an integer) are considered antiaromatic and are typically less stable due to electron delocalization that leads to increased ring strain. Non-aromatic compounds, on the other hand, do not meet the criteria of cyclic, planar, conjugated systems with delocalized π-electrons and do not follow the 4n+2 rule.

 

Why 4n+2 π electrons?

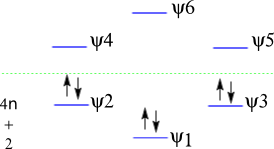
Recall from the discussion of the Frost Circle Mnemonic that we can easily construct the MO energy levels of a cyclic conjugated system by placing the polygon (hexagon for benzene) such that one corner is pointing down.  Below is the MO energy diagram for benzene.  As long as at least one energy level is full then the system is stable or aromatic.  The lowest energy level can only ever hold a maximum of two electrons (ψ1), while the degenerate ψ2 and ψ3 can hold a maximum of 4 electrons.  Therefore in order to be aromatic there must be 4n+2 π electrons.

 

Going Deeper

The rule in Hückel's theory for aromaticity is derived from quantum mechanical principles, specifically from the solutions to the Schrödinger equation for a conjugated cyclic molecule, such as a benzene ring. Erich Hückel developed this rule in the early 20th century as part of his molecular orbital theory to explain the stability of benzene and similar compounds.

In a conjugated π system, the π electrons can be delocalized around the ring, creating a set of molecular orbitals that can be occupied by these electrons. According to quantum mechanics, these molecular orbitals have different energy levels. For a molecule to be aromatic and thus exceptionally stable, it must have its π\pi electrons completely fill a set of bonding molecular orbitals, leaving no bonding orbitals partially filled and no antibonding orbitals filled. This condition leads to an overall lower energy state for the molecule.

The derivation of the 4n+2 rule is based on the way these molecular orbitals fill up in a cyclic, conjugated system:

  • The lowest energy state, or the ground state, of a molecule occurs when all its electrons are in the lowest possible energy levels (orbitals).
  • In a cyclic, conjugated π system, the molecular orbitals can be described as a series of standing waves around the ring. For the system to be especially stable (aromatic), these standing waves must be completely constructive around the ring, leading to no nodes (points of zero electron density) in the cycle of delocalization, apart from those required by the molecular geometry.
  • For a constructive standing wave to form around a cyclic molecule, the number of wavelength components (which correspond to the π\pi electrons) must be such that they constructively interfere. This condition is met when the number of π\pi electrons follows the formula.
  • Mathematically, this comes from the boundary conditions imposed by the cyclic nature of the molecule, where is a non-negative integer (0, 1, 2, 3, ...). The +2 arises from the requirement for at least one fully constructive wave (with two electrons, since each molecular orbital can hold two electrons with opposite spins) to stabilize the ring. The 4n part allows for the addition of pairs of electrons that maintain the constructive interference pattern around the ring.

Thus, the 4n+2 rule is a direct consequence of the quantum mechanical treatment of electrons in a cyclic, conjugated system, reflecting the conditions under which these systems can achieve maximal stability through the delocalization of π electrons.