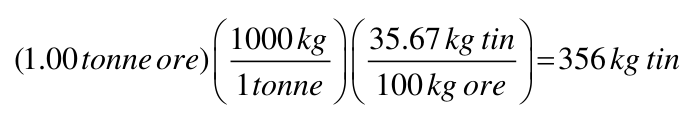- 1. Getting Started
-
2.
First Semester Topics
-
General Chemistry Review
- Introduction
- Electron Configurations of Atoms
- QM Description of Orbitals
- Practice Time - Electron Configurations
- Hybridization
- Closer Look at Hybridization
- Strategy to Determine Hybridization
- Practice Time! - Hybridization
- Formal Charge
- Practice Time - Formal Charge
- Acids-bases
- Practice Time - Acids and Bases
- Hydrogen Bonding is a Verb!
- Progress Pulse
-
Structure and Bonding
- Chemical Intuition
- From Quantum Mechanics to the Blackboard: The Power of Approximations
- Atomic Orbitals
- Electron Configurations of Atoms
- Electron Configurations Tutorial
- Practice Time - Structure and Bonding 1
- Lewis Structures
- Drawing Lewis Structures
- Valence Bond Theory
- Valence Bond Theory Tutorial
- Hybridization
- Polar Covalent Bonds
- Formal Charge
- Practice Time - Structure and Bonding 2
- Curved Arrow Notation
- Resonance
- Electrons behave like waves
- MO Theory Intro
- Structural Representations
- Progress Pulse
-
Acids/Base and Reactions
- Reactions
- Reaction Arrows: What do they mean?
- Thermodynamics of Reactions
- Acids Intro
- Practice Time! Generating a conjugate base.
- Lewis Acids and Bases
- pKa Scale
- Practice Time! pKa's
- Predicting Acid-Base Reactions from pKa
- Structure and Acidity
- Structure and Acidity II
- Practice Time! Structure and Acidity
- Curved Arrows and Reactions
- Nucleophiles
- Electrophiles
- Practice Time! Identifying Nucleophiles and Electrophiles
- Mechanisms and Arrow Pushing
- Practice Time! Mechanisms and Reactions
- Energy Diagrams and Reactions
- Practice Time! - Energy Diagrams
- Progress Pulse
- Introduction to Retrosynthesis
-
Alkanes and Cycloalkanes
- Introduction to Hydrocarbons and Alkanes
- Occurrence
- Functional Groups
- Practice Time! Functional Groups.
- Structure of Alkanes - Structure of Methane
- Structure of Alkanes - Structure of Ethane
- Naming Alkanes
- Practice Time! Naming Alkanes
- Alkane Isomers
- Relative Stability of Acyclic Alkanes
- Physical Properties of Alkanes
- Ranking Boiling Point and Solubility of Compounds
- Conformations of Acyclic Alkanes
- Practice Time! Conformations of acyclic alkanes.
- Conformations of Cyclic Alkanes
- Naming Bicyclic Compounds
- Stability of Cycloalkane (Combustion Analysis)
- Degree of Unsaturation
-
Stereochemistry
- Enalapril in ACE
- Constitutional and Stereoisomers
- Chirality or Handedness
- Drawing a Molecules Mirror Image
- Exploring Mirror Image Structures
- Enantiomers
- Drawing Enantiomers
- Practice Time! Drawing Enantiomers
- Identifying Chiral Centers
- Practice Time! Identifying Chiral Molecules
- CIP (Cahn-Ingold-Prelog) Priorities
- Determining R/S Configuration
- Diastereomers
- Meso Compounds
- Fischer Projections
- Fischer Projections: Carbohydrates
- Measuring Chiral Purity
- Practice Time! - Determining Chiral Purity and ee
- Chirality and Drugs
- Chiral Synthesis
- Prochirality
- Converting Fischer Projections to Zig-zag Structures
- Practice Time! - Assigning R/S Configurations
-
Alkenes and Addition Reactions
- The Structure of Alkenes
- Alkene Structure - Ethene
- Physical Properties of Alkenes
- Naming Alkenes
- Health Insight - BVO (Brominated Vegetable Oil)
- E/Z and CIP
- Stability of Alkenes
- H-X Addition to Alkenes: Hydrohalogenation
- Practice Time - Hydrohalogenation
- X2 Addition to Alkenes: Halogenation
- HOX addition: Halohydrins
- Practice Time - Halogenation
- Hydroboration/Oxidation of Alkenes: Hydration
- Practice Time - Hydroboration-Oxidation
- Oxymercuration-Reduction: Hydration
- Practice Time - Oxymercuration/Reduction
- Oxidation and Reduction in Organic Chemistry
- Calculating Oxidation States of Carbon
- Identifying oxidation and reduction reactions
- Practice Time - Oxidation and Reduction in Organic
- Oxidation
- Reduction
- Capsaicin
-
Alkynes
- Structure of Ethyne (Acetylene)
- Naming Alkynes
- Practice Time! - Naming Alkynes
- Physical Properties of Alkynes
- Preparation of Alkynes
- Practice Time! - Preparation of Alkynes
- H-X Addition to Alkynes
- X2 Addition
- Hydration
- Reduction of Alkynes
- Practice Time! - Addition Reactions of Alkynes
- Oxidative Cleavage of Alkynes
- Alkyne Acidity and Acetylide Anions
- Reactions of Acetylide Anions
- Retrosynthesis Revisted
- Practice Time! - Multistep Synthesis Using Acetylides
-
Alkyl Halides and Alcohol
- Naming Alkyl Halides
- Naming Alcohols
- Classes of Alcohols and Alkyl Halides
- Practice Time! - Naming Alkyl Halides
- Practice Time! - Naming Alcohols
- Physical Properties of Alcohols and Alkyl Halides
- Structure and Reactivity of Alcohols
- Structure and Reactivity of Alkyl Halides
- Preparation of Alkyl Halides and Tosylates from Alcohols
- Practice Time! - Alcohols to Alkyl Halides
- Preparation of Alkyl Halides from Alkenes; Allylic Bromination
- Strategy for Predicting Products of Allylic Brominations
- Practice Time! - Allylic Bromination
-
Substitutions (SN1/SN2) and Eliminations (E1/E2)
- Introduction
- Solvents
- SN1 Reaction: The Carbocation Pathway
- SN2 Reactions: The Concerted Backside Attack
- SN1 vs. SN2: Choosing the Right Path
- Application: Cardura (Doxazosin)
- E1 Reactions: Elimination via Carbocations
- E2 Reactions: The Concerted Elimination
- E1cB: The Conjugate Base Elimination Pathway
- Substitution versus Elimination
- Dienes, Allylic and Benzylic systems
-
General Chemistry Review
-
3.
Second Semester Topics
- Arenes and Aromaticity
-
Reactions of Arenes
- Electrophilic Aromatic Substitution
- EAS-Halogenation
- EAS-Nitration
- Practice Time - Synthesis of Aniline
- EAS-Alkylation
- Practice Time - Friedel Crafts Alkylation
- EAS-Acylation
- Practice Time - Synthesis of Alkyl Arenes
- EAS-Sulfonation
- Practice Time - EAS
- Donation and Withdrawal of Electrons
- Regiochemistry in EAS
- Practice Time - Directing Group Effects
- Synthesizing Disubstituted Benzenes: Effects of Substituents on Rate and Orientation
- Steric Considerations
- Strategies for Synthesizing Disubstituted Benzenes
- NAS - Addition/Elimination
- NAS - Elimination/Addition - Benzyne
- Alcohols and Phenols
-
Ethers and Epoxides
- Intro and Occurrence
- Crown Ethers and Cryptands
- Preparation of Ethers
- Reactions of Ethers
- Practice Time - Ethers
- Preparation of Epoxides
- Reactions of Epoxides - Acidic Ring Opening
- Practice Time - Acidic Ring Opening
- Reactions of Epoxides - Nucleophilic Ring Opening
- Practice Time - Nucleophilic Ring opening
- Application - Epoxidation in Reboxetine Synthesis
- Application - Nucleophilic Epoxide Ring Opening in Crixivan Synthesis
- Physical Properties of Ethers and Epoxides
- Naming Ethers and Epoxides
-
Aldehydes and Ketones
- Naming Aldehydes and Ketones
- Physical Properties of Ketones and Aldehydes
- Practice Time - Naming Aldehydes/Ketones
- Nucleophilic addition
- Addition of Water - Gem Diols
- Practice Time - Hydration of Ketones and Aldehydes
- Addition of Alcohols - Hemiacetals and Acetals
- Acetal Protecting Groups
- Hemiacetals in Carbohydrates
- Practice Time - Hemiacetals and Acetals
- Addition of Amines - Imines
- Addition of Amines - Enamines
- Practice Time - Imines and Enamines
- Application - Imatinab Enamine Synthesis
- Addition of CN - Cyanohydrins
- Practice Time - Cyanohydrins
- Application - Isentress Synthesis
- Addition of Ylides - Wittig Reaction
- Practice Time - Wittig Olefination
- Structure of Ketones and Aldehydes
- Carboxylic Acids and Derivatives
- Enols and Enolates
- Condensation Reactions
-
4.
NMR, IR, UV and MS
- Spectroscopy
-
HNMR
- Nuclear Spin
- Interpreting
- Chemical Shift
- Practice Time! - Chemical Shift
- Equivalency
- Indentifying Homotopic, Enantiotopic and Diastereotopic Protons
- Practice Time! - Equivalency
- Intensity of Signals
- Spin Spin Splitting
- Practice Time! - Spin-Spin Splitting
- Primer on ¹³C NMR Spectroscopy
- Alkanes
- Alkynes
- Alcohols
- Alkenes
- Coupling in Cis/Trans Alkenes
- Ketones
- HNMR Practice 1
- HNMR Practice 2
- HNMR Practice 3
- HNMR Practice 4
- Exchangeable Protons and Deuterium Exchange
- IR - Infrared Spectroscopy
- UV - Ultraviolet Spectroscopy
- Mass Spectrometry
-
5.
General Chemistry
- General Chemistry Lab
- Strategy for Balancing Chemical Reactions
- Calculator Tips for Chemistry
- Significant Figures
- Practice Time! Significant Figures
- Spreadsheets - Getting Started
- Spreadsheets - Charts and Trend lines
- Standard Deviation
- Standard Deviation Calculations
- Factor Labels
- Practice Time! - Factor Labels
- Limiting Reagent Problem
- Percent Composition
- Molar Mass Calculation
- Average Atomic Mass
- Empirical Formula
- Practice time! Empirical and Molecular Formulae
- Initial Rate Analysis
- Practice Time! Initial Rate Analysis
- Solving Equilibrium Problems with ICE
- Practice Time! Equilibrium ICE Tables
- Le Chatelier's
- Practice Time! Le Chatelier's Principle
- 6. Organic Chemistry Lab
- 7. Tools and Reference
-
8.
Tutorials
- Reaction Mechanisms (introduction)
- Factor Labels
- Acetylides and Synthesis
- Drawing Cyclohexane Chair Structures
- Drawing Lewis Structures
- Aromaticity Tutorial
- Common Named Aromatics (Crossword Puzzle)
- Functional Groups (Flashcards)
- Characteristic Reactions of Functional Groups
- Alkyl and Alkenyl Groups
- Valence Bond Theory
- Alkane Nomenclature
-
9.
The Alchemy of Drug Development
- Ivermectin: From Merck Innovation to Global Health Impact
- The Fen-Phen Fix: A Weight Loss Dream Turned Heartbreak
- The Asymmetry of Harm: Thalidomide and the Power of Molecular Shape
- Semaglutide (Ozempic): From Lizard Spit to a Once-Weekly Wonder
- From Cocaine to Novocain: The Development of Safer Local Anesthesia
- The Crixivan Saga: A Targeted Strike Against HIV
- The story of Merck’s COX-2 inhibitor, Vioxx (rofecoxib)
- The Accidental Aphrodisiac: The Story of Viagra
- THC: A Double-Edged Sword with Potential Neuroprotective Properties?
- Ritonavir Near Disaster and Polymorphism
Clear History
Factor Labels
The Factor-Label Method is a very important concept in science. While it may "feel" strange at first, once you gain experience, you will agree that it makes calculations much simpler! In this technique, all measurements and conversion factors are represented as fractions. The investigator, must decide a starting point and an ending point of the calculations. They then add factors, cancelling units, until the starting unit is been converted into the ending unit. Once the factors are arranged correctly, all numerators are multiplied and denominators are divided.
For example, the density of a solid may have a value of 1.35 g/mL. This could be written as:
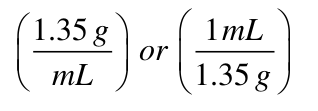
The first case would indicate multiplication of the density with "1.35 g" as the numerator and "mL" as the denominator. Although, if we decided to divide by the density, the second inverted case would be used with '1 mL' being the new numerator and '1.35 g' being the new denominator.
Therefore, in the Factor-Label method each factor is analyzed one step at a time so that the overall units, after cancelation, are converted from the starting measurement to the ending result. Once the factors are all in place, the numerators are then multiplied and the denominators are divided.
For example, optical fibers 0.10 mm thick can be inserted into a patient’s vein and maneuvered to the heart, where they deliver laser light that breaks up blood clots. What is the thickness of these optical fibers in inches?
i) the conversion is mm to inches.
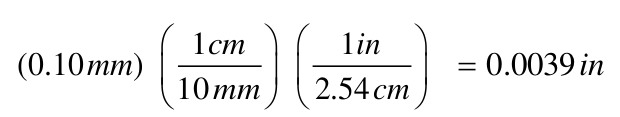
Write the starting measurement (0.10 mm), convert "mm to cm" and finally convert "cm into in". Ignoring any multiplication or division by '1', the final result would be found by entering '0.10' in the calculator and dividing by '10' and then dividing by '2.54'. The final result '0.0039' must be accompanied by units or it is meaningless!
A second harder example is as follows (don't worry if you don't understand the chemistry, concentrate on the mathematics), what is the new concentration of HCl if 35.0 mL of 0.250 mol HCl/L solution are diluted to 0.500 L?
Starting value is '35.0 mL' of solution, convert 'mL to L', covert 'L to moles HCl' and then DIVIDE by final volume '0.500 L'. Notice, when you need to divide, place the value to be divided in the denominator.
Using Percentages in Factor Label
Percentages should always be represented as parts per hundred in Factor Label problems. For example if a compound is 25.0 % (m/m) sodium. (m = mass, v = volume) the factor used should be either
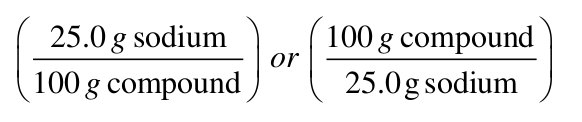
Here is an example, An ore of tin contains 35.67 % (m/m) tin. If you need to obtain 45.3 g of tin, how many kilograms of ore must be refined? Assume 100 % recovery of the tin.
First write the percentage as a factor.
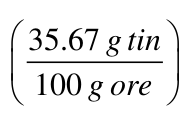
Next decide the starting and ending units of the problem. The starting value is almost always something you can touch or pick up. In this case it is 45.3 g of tin. The ending needs to be in "kg ore" (defined by problem!).
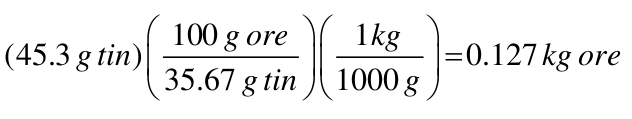
The mathematics would be 45.3 multiplied by 100, divided by 35.67, divided by 1000. Notice, '1''s are ignored for they are the identity element and don't change the overall values!
For a second example,
How many kilograms of Tin are present in 100.0 kg of tin ore (the ore contains 35.67 % (m/m) tin).
Note, the % (m/m) indicates ANY unit mass. In the above example, grams were used. In this example, kg are used. It does not matter as long as you are consistent.