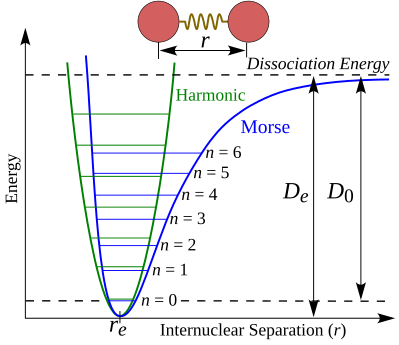
Harmonic Oscillator

Quantum Mechanical Harmonic Oscillator

The quantum harmonic oscillator is a fundamental model in quantum mechanics describing a particle in a potential well, commonly used to approximate molecular vibrations. Its potential energy function is the same as the classical case:

$$V(x) = \frac{1}{2} k x^2$$

Where:

• $V(x)$: Potential energy as a function of displacement $x$.
• $k$: Force constant (bond stiffness).
• $x$: Displacement from equilibrium (assumed equilibrium at $x = 0$).

The quantum mechanical solution involves solving the Schrödinger equation:

$$\hat{H} \psi_n(x) = E_n \psi_n(x)$$

Where $\hat{H}$ is the Hamiltonian operator, $\psi_n(x)$ are the wavefunctions, and $E_n$ are the quantized energy levels.

Quantized Energy Levels

The allowed energy levels are given by:

$$E_n = \hbar \omega \left( n + \frac{1}{2} \right)$$

Where:

• $n$: Quantum number ($n = 0, 1, 2, \dots$).
• $\hbar$: Reduced Planck's constant.
• $\omega = \sqrt{k/m}$: Angular frequency of the oscillator.
• $m$: Mass of the particle.

Key features:

• The lowest energy level ($n = 0$) is not zero; instead, it is the zero-point energy ($\frac{1}{2} \hbar \omega$).
• Energy levels are evenly spaced by $\hbar \omega$.

Wavefunctions ($\psi_n(x)$)

The wavefunctions $\psi_n(x)$ are solutions to the Schrödinger equation, and they correspond to the probability distributions of the particle at each energy level. They are expressed in terms of Hermite polynomials $H_n(x)$:

$$\psi_n(x) = N_n e^{-\frac{\alpha x^2}{2}} H_n(\sqrt{\alpha} x)$$

Where:

• $\alpha = \frac{m \omega}{\hbar}$: A scaling factor based on mass and angular frequency.
• $N_n$: Normalization constant ensuring total probability equals 1.
• $H_n$: Hermite polynomials.

Key Differences From Classical Behavior:

• In classical mechanics, the particle oscillates continuously within the potential well, with all energy levels being possible.
• In quantum mechanics:
  • The energy is quantized.
  • The particle has a nonzero probability of being found outside the classical turning points due to quantum tunneling.
  • Zero-point energy prevents the particle from being at rest at $x = 0$.